О качестве перемещения объекта позиционирующей системой можно судить по точности позиционирования, точности повторяемости и углу отклонения. Самый критический аспект системы, если говорить о ее точности, это вид привода. Для преобразования вращения двигателя в линейное движение каретки в приводной системе используются шарико-винтовые пары, трапецеидальная резьба или зубчатые ремни. Кроме привода, крепеж и профиль линейных элементов также могут быть причиной ошибок точности. Следствием может быть угловое отклонение, негативно влияющее на общую точность системы. Неточности в приводных системах можно объяснить следующими причинами:
Ошибки кинематики
Кинематические ошибки позиционирования возникают, по существу, из-за погрешности шага ходового винта. Они сказываются непосредственно на результатах измерения.
Мертвый ход
Ошибки реверса при позиционировании могут иметь различную природу. Причинами могут быть зазоры и эластичность в сочетании с силами трения. Так называемая ошибка накопления вследствие смещения шарика при запуске шарико-винтовой пары с прецизионным преднатягом (с двумя точками контакта) также может приводить к ошибкам порядка 1 - 10 мкм.
Деформация механизма подачи под воздействием динамических сил
К изменению механизма подачи, по существу, приводят: инерционная сила при разгоне салазок, силы обусловленные технологическим процессом (если имеются) и силы трения в направляющих. Они приводят к смещению действительного положения линейных элементов относительно заданной позиции.
Силы ускорения
Типовая масса салазок и умеренное ускорение 2 м/с² приводят к отклонению в значениях перемещений от 5 до 10 микрометров, не распознаваемому системой вращения винт-привод. При более высоких значениях ускорения возрастает и отклонение.
Силы трения
Значения сил трения в направляющих, в зависимости от типа установки составляют от 1 % до 2 % нормальной составляющей силы для роликовых направляющих и от 3 % до 12 % нормальной составляющей силы в случае направляющих скольжения. Таким образом, при величине нормальной составляющей силы в 500 N деформация механизма подачи в следствии сил трения столь незначительны, что ими можно пренебречь.
Трение в гайке ходового винта
Как правило, в гайке ходового винта возникает большая часть трения системы подачи. Причина этого кроется в сложной кинематике гайки. На первый взгляд, вопреки движению качения шариков, происходит значительный вклад в трение скольжения. Наряду с микрозначениями пробуксовки вследствие относительного движения в деформированной зоне контакта, возникает и макропробуксовка вследствие ограниченных кинематических условий. Шарики не являются полностью ведомыми в канавках резьбы и испытывают биение, как „теннисные мячи в водосточной трубе". Следствием является постоянное столкновение и сдвиги шариков, а также их проскальзывание. Имеет место значительное трение между шариками из-за высокого удельного давления вследствие безсепараторного перемещения. Как и в любом радиально-упорном шарикоподшипнике возникает трение кручения из-за неперпендикулярно расположенной к оси вращения окружности касания шариков. Каждый шарик вращается в плоскости окружности касания. Новые исследования указывают на то, что движение шариков в резьбе возможно только из-за дополнительного скольжения, обусловленного шагом резьбы. Система возврата - особая проблемная зона приводов с шариково-винтовой парой. При каждом входе шарика в систему возврата, также как и при выходе из нее, характер движения шарика полностью изменяется. Среди прочего, энергия вращения шарика каждый раз должна заново возобновляться и гаситься. В противоположность нагруженному участку резьбы, шарики, поступая в систему возврата, не так ограничены в движении. Таким образом, исходя из соображения энергозатрат, система возврата является предпочтительным местом нахождения шариков. Без различных специальных приёмов для возврата шариков в резьбу в конце системы возврата, неизбежен затор шариков, который может привести к её полному зажиму.
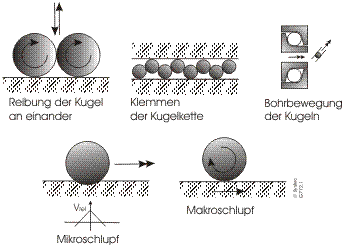
Анализ ошибок
Основные определения:
Измерение физической величины означает экспериментальное нахождение значения этой величины в заданных единицах. Точное (истинное) значение измерения определить невозможно, поскольку не существует измерений без ошибок. Таковыми являются:
| Тип ошибки | Причина |
| Инструментальная ошибка | Неправильная калибровка |
| Человеческий фактор | Неверное считывание результатов, помехи |
| Методические ошибки | Некорректное проведение измерения |
Все ошибки можно разделить на систематические и статистические.
О систематической ошибке говорят, если при каждом измерении в одинаковых условиях результат отличается от правильного значения в одну сторону и на одинаковую величину. Эту ошибку можно заметить только в случае, если правильный результат известен. Типичной систематической ошибкой является погрешность градуировки измерительного прибора.
Как только систематические ошибки распознаны и при помощи метода сложения максимальных значений ошибок учтены их пределы, истинное значение величины измерения (без учета статистических ошибок) находится между E - ΔE и E + ΔE.
При статистической ошибке проведение повторного замера той же самой величины измерения при казалось бы неизменных условиях измерения не всякий раз будет приводить к повторению результата. Это можно объяснить различными факторами: например, трением, установкой отличной от оптимальной и т.д.
Многие причины статистических ошибок непосредственно измеряемых величин влияют друг на друга и приводят к результатам, отличающимся от измерения к измерению. Многократное повторение измерений позволяет более точно определить среднее значение величины. Серийные измерения величины позволяют определить не только ее среднее (арифметическое) значение, но и оценить достоверность измерения, вычислив среднеквадратичное отклонение.
Оценить статистическую ошибку можно на основании величин „среднего значения", „средне-квадратичного отклонения" и „доверительного интервала".
Среднее значение
Среднее значение величины серии из n измерений xi рассчитывается по следующей формуле
Формула 1
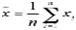 Вычисленное таким образом из конечного числа измерений среднее значение величины тем точнее приближается к истинному среднему значению µ, чем большее количество измерений n проводится.
Вычисленное таким образом из конечного числа измерений среднее значение величины тем точнее приближается к истинному среднему значению µ, чем большее количество измерений n проводится.
Формула 2
 Если истинное значение известно, то случайную ошибку Er конечного ряда измерений можно вычислить как разность
Если истинное значение известно, то случайную ошибку Er конечного ряда измерений можно вычислить как разность
Поскольку на практике обычно имеют дело с конечным малым количеством измерений, а истинное значение неизвестно, все вычисления проводятся при помощи среднего значения .
Среднеквадратичное отклонение
Среднеквадратичное отклонение служит мерой вариабельности величины измерения. Каждое отдельное измерение xi отклоняется случайным образом от среднего значения. Диапазон, в который попадают все измерения, определяется как среднеквадратичное отклонение s. Среднеквадратичное отклонение s ряда измерений с n значениями вычисляется как квадратный корень из отдельных квадратичных отклонений, разделенных на (n-1). Измеряется в тех же единицах, что и сами величины.
Формула 3
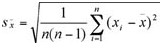
Другая иногда используемая величина, относительное среднеквадратичное отклонение Sr, рассчитывается по следующей формуле:
Формула 4
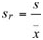 Нормальное распределение
Нормальное распределение
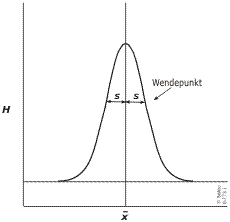
При достаточно большом количестве измерений, некоторые значения встречаются чаще других, а некоторые, наоборот, весьма редко. Как правило, среднее значение встречается чаще остальных, а предельные - реже всех. Если в системе координат по оси абсцисс (x-оси) отложить значения измерений, а по оси ординат (y-оси) частоту встречаемости, то значения, как правило, скапливаются в средней части, а по мере удаления от среднего значения симметрично убывают. Образуется симметрично спадающая колоколообразная кривая с одной вершиной.
Этот случайный разброс последовательности измерений во многих случаях подходит под так называемое нормальное распределение. Оно устойчиво, симметрично и однозначно определено средним значением µ и среднеквадратичным отклонением σ. Серия измерений с конечным n не позволяет точно определить µ и σ, их заменяют и s.
Расчет погрешностей
Значение экспериментально определяемой физической величины в большинстве случаев невозможно определить непосредственно, поскольку специальное оборудование не существует или недоступно. Необходимо измерить значение нескольких величин, которые, при подстановке в соответствующие физические формулы, дают возможность расчета искомой величины. Этот подход носит название косвенного метода измерения.
Если результат измерения есть функция нескольких измеренных величин, применяется правило расчета погрешностей. При расчете ошибки делят на систематические и случайные .
Систематические ошибки:
Систематические ошибки могут компенсировать друг друга. Малое количество систематических ошибок может сдвинуть результат в каком-то одном направлении. Этот случай даже более вероятен. Поэтому частичная компенсация систематических ошибок обычно не учитывается, а распространение погрешностей вычисляют при помощи сложения максимальных значений ошибок, которое, в свою очередь, является полным дифференциалом с суммированием по модулю. Систематическая ошибка Δy функции y = F (x1... xn) рассчитывается по следующей формуле:
Формула 5
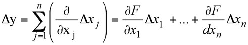 Статистическая ошибка:
Статистическая ошибка:
Поскольку систематическая ошибка с равной вероятностью как уменьшает, так и увеличивает измеряемую величину, т.е. имеет место взаимная частичная компенсация ошибок, входящих в конечный результат, существует формула, учитывающая этот эффект. Если при нормальном распределении измеряемой величины известны стандартные отклонения s1...sn независимых друг от друга значений x1...xn, то стандартное отклонение результата измерения рассчитывается по следующей формуле:
Формула 6
Результат измерения y = F (x1…xj…xn)
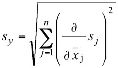
Точность приводной системы:
При обсуждении точности приводной системы важны следующие термины:
| Параметр | Определение | Фактор влияния |
| Точность позиционирования | Максимальное отклонение между истинной и реальной позицией |
Точность линейного элемента, привода, двигателя дефекты винтовой пары, люфт в системе |
| Точность повторяемости | Способность системы многократно достигать заданную позицию в одном и том же направлении | Точность повторяемости линейного элемента/двигателя, трение |
| Разрешение | Минимальный достижимый прирост позиционирования |
Угловое разрешение двигателя, передаточное число, шаг резьбы |
| Мертвый ход | "Мертвое пространство" между движущимися частями | Износ/слабина между движущимися частями |
Абсолютная точность
Абсолютная точность указывает на отклонение между ожидаемой заданной позицией и средним значением реального положения, которое получается в процессе посещения заданной позиции с различных сторон(мультинаправленно). Термин "абсолютный" выражает отношение характеризующей величины к базовой системе координат системы. Абсолютную точность определяют как разницу заданного и реального положения системы позиционирования. Она описывается через среднее значение рассеивания плюс его диапазон.
Формула 7
G = ΔP ± R
Где: ΔP расстояние между заданной позицией и средним значением рассеивания.
R - диапазон рассеивания.
Точность повторяемости
Точность повторяемости указывает, насколько точно приводная система позиционирует при перемещении в одном и том же направлении и определяется как усредненное отклонение между заданным и реальным значением. Измерить точность повторяемости можно без привязки к системе координат, поскольку заданная позиция для сравнения не требуется. Наряду с однонаправленной точностью повторяемости, в специальных случаях говорят о двунаправленной точности повторяемости, когда перемещение в заданную позицию происходит с двух сторон.
Точность повторяемости - важная величина для описания позиционирующей системы. Она определяет разброс относительно среднего значения при множественном позиционировании. Разброс позиций описывается гауссовым или "нормальным" распределением. Среднеквадратичное отклонение - самый распространенный способ описания разброса для такого распределения. Стабильность определяется с помощью трех стандартных отклонений, т.н. « правило 3σ » с вероятностью 99,74% (следуя принятому в ISO определению).

Рис. 3
Нормами, определяющими точность системы приводов, являются:
- ISO 230-2;
- ASME B5.54.
Оценка ошибок позиционирования системы приводов
Разбор ошибок позиционирования является комплексной задачей и находится в тесной связи со структурой системой. Оценку точности проведем на следующем примере.
В нём мы рассмотрим 3-х координатную систему позиционирования (см. рис. 4). Влияние всех системных ошибок, в конечном счете, сконцентрировано на одной точке „самого внутреннего" линейного элемента. На данной точке приложения системы или центральной координате инструмента системы(Tool Center Point, TCP) закреплен груз(рабочий инструмент, в случае станка). Суммарную ошибку в этой точке системы можно разделить на компоненты пространственного вектора (x, y, z). В этом примере предположим, что TCP находится на конце оси Z. Компоненты пространственного вектора состоят из:
- Ошибка по направлению оси X;
- Ошибка по направлению оси Y;
- Ошибка по направлению оси Z.
Каждая из этих ошибок имеет статическую и динамическую составляющие.
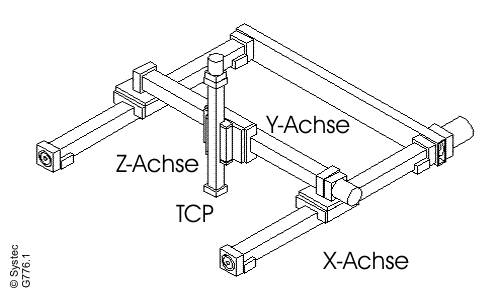
Рис. 4 Пример для расчета точности некой системы
- Разбор статических ошибок в направлении оси X
- Оценим возможный «перекос» оси Y. Пара кареток оси x перемещается не абсолютно синхронно. Следствием этого является смещение оси Y, которая отклоняется в плоскости оси X. Эту ошибку можно рассчитать при помощи подобных треугольников.
- Ошибка позиционирования по оси X есть сумма ошибки позиционирования привода плюс ошибок вследствие люфта оси Y.
- Теоретически, существует еще одна ошибка, влияющая на смещение из-за вертикального положения оси Z. Соответственно, эта ошибка вносит свой вклад в компоненты ошибок осей X и Y. Эта ошибка пренебрежимо мала и на практике не учитывается.
- Статическая суммарная ошибка по направлению движения оси X, таким образом, есть сумма ошибки позиционирования линейного элемента, служащего осью X, и ошибки «перекоса» оси Y.
- Разбор статических ошибок при движении по оси Y
- Статическая суммарная ошибка при движении оси Y, таким образом, есть ошибка позиционирования линейного элемента, служащего осью Y.
- Разбор статических ошибок при движении по оси Z
Статическая суммарная ошибка при движении оси Z состоит из следующих компонент:
ошибка позиционирования линейного элемента, служащего осью Z
максимальный прогиб оси X
максимальный прогиб оси Y
Прогиб зависит от геометрии, типа и материала линейного элемента, а также от позиции нагрузки. Приближение прогиба можно рассчитать по следующей формуле:
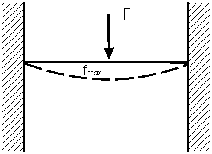
Рис. 5
где
F - сила [N]
L - расстояние между опорами [m]
E - модуль эластичности [N/mm²]
I - момент инерции площади [cm4 ]
Динамическая составляющая ошибки
При коротких рабочих циклах время восстановления системы сокращается. При этом могут возникнуть ошибки точности, которые объясняются инерционными силами. Их можно учесть, представив прогиб как результат совместного действия статических сил и сил инерции.
Общая методика разбора позиционируемости линейных модулей
Для каждого линейного элемента проводится по 9 серий измерений. Временной интервал между двумя измерениями - 1 час. Каждая серия измерений состоит из 10(или >10) последовательных измерений позиций в трех положениях: 1/5, 1/2 и 4/5 длины прохода. При этом вычисляют значения для следующих величин:
- Среднеквадратичное отклонение ошибки позиционирования: среднее значение отклонения при каждом из 10 измерений - Mi
- Поле рассеивания: +/- 3 кратное среднеквадратичное отклонение десяти измерений.
- Максимальное и минимальное среднее отклонение: Mi min; Mi max для каждой из трех позиций.
- Среднеквадратичное отклонение из 90 измерений для каждой из трех заданных позиций.
- Для каждой из трех позиций строится следующий график:
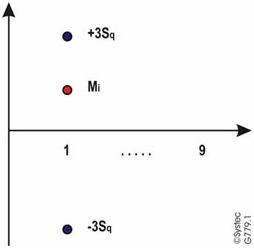
Рис. 6
- Выясняются максимальное и минимальное отклонения для каждой серий измерений:
max M = Mi max + 3S²q ; min M = Mi min - 3S²q
Максимальное рассеивание для каждой из позиций - разность между max. M и min. M. - Максимальная ошибка ошибка позиционирования (абсолютная точность) - это
max abs (max M, min M).
Источник - industrialauto.ru