ДЕМПФИРОВАНИЕ КОЛЕБАНИЙ В СТАНИНАХ МЕТАЛЛОРЕЖУЩИХ СТАНКОВ С ЧПУ. Математическое моделирование
Силы, возникающие при резании, состоят из статической и динамической компоненты, причем динамическая имеет ярко выраженный периодический характер и имеет широкий диапазон возбуждающих частот. Если конструкция станины возбуждается на частоте близкой к собственной частоте колебаний или вблизи нее, то амплитуда колебаний может на несколько порядков превышать амплитуду статических отклонений при работе станка. Результатом такого усиления будет вибрация, которая может серьезно повлиять на качество работы и продукции.
4.1 Математические модели
Для того чтобы получить представление о динамических свойствах конструкции, полезно начать изучение с поведения системы «масса-пружина» с одной степенью свободы, к которой присоединен гаситель (демпфер) колебаний. Уравнение движения такой системы может быть записано в следующем виде:
где m – масса, а k – коэффициент упругости пружины.
Мы можем переписать уравнение, 4.1 введя в него резонансную частоту -
передаточная которого, используя преобразование Лапласа, может быть записана как:
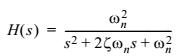 (4.3)
(4.3)Данное уравнение имеет три различных решения для таких значений коэффициента демпфирования: 0<ζ<1, ζ=1 и ζ>1. Первое решение называется подкритическое демпфирование, когда коэффициент демпфирования лежит в интервале 0<ζ<1 и такое решение является наиболее подходящим для описания демпфирования колебаний в механических системах. Отклик такой подкритически демпфированной системы [Franklin et al] описывается следующим образом:
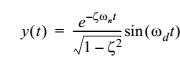 , где
, где На рисунке 4.1 показан отклик системы второго порядка с различными значениями коэффициента демпфирования. Недемпфированная система (ζ=0) не смогла бы рассеивать механическую энергию и сохраняла бы колебания вечно. Например, сталь имеет очень незначительное собственное демпфирование и может быть смоделирована с коэффициентом демпфирования, лежащим в диапазоне 0,0004-0,0007 [Slocum (a)].
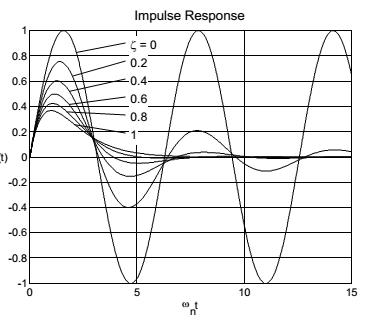
Рис. 4.1 Отклик системы второго порядка на механический импульс.
Коэффициент демпфирования ζ определяет насколько быстро будет ослабляться отклик системы и эффект его влияния показан на рисунке 4.2. Для значения коэффициента демпфирования равного ζ<1 отклик системы будет колебаться около нуля и в итоге полностью затухнет. Критически демпфированная система (ζ=1) и сверхдемпфированная система (ζ>1) не имеют таких «выбросов», а амплитуда движения системы асимптотически приближается к нулю. Приняв производную y(t) равной нулю мы можем рассчитать время нарастания колебания tp
где ωd – собственная частота демпфированной системы. Используя уравнение 4.4, можно рассчитать демпфирующий коэффициент:
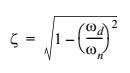 (4.6)
(4.6)Структура реального станка намного сложнее простой системы масса-пружина описанной в разделе 4.1 и модели вязкостного демпфирования используемая для определения уравнения движения, описанного в ур-е 4.1. Упрощенный подход для описания демпфирования такой системы – введение коэффициента потерь η, который определяется отношением между средней энергией рассеянной на радиан к пиковому значению потенциальной энергии в цикле [Nayfeh]. При резонансе коэффициент потерь становится равен … . Демпфирование также может быть описано при помощи коэффициента добротности Q, который представляет собою усиление системы колеблющейся на резонансной частоте и рассчитывается как величина обратная коэффициенту потерь η. Не смотря на то, что реальные конструкции состоят из большого количества систем «масса-пружина» и, следовательно, характеризуются большим числом резонансных частот, ур-е 4.1 также может быть использовано для иллюстрации идеи о максимизации жесткости системы и минимизации ее массы, с целью получения высокой первой частоты собственных колебаний. В тоже время, частоты возмущающих воздействий могут быть выше первой моды и в таком случае в конструкции возбуждаются более высокие, но гораздо менее сильные моды. При изучении динамики машин низкие моды представляю особый интерес, так как им свойственно иметь наибольшую энергию.
> Демпфирование колебаний: Часть 2.